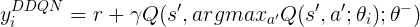Wang, de Freitas, Lanctot, 2016

Summary

For many states, it is unnecessary to estimate the action value for each action. This is a problem with methods that attempt to favor exploration over exploitation too much, because often times there will be a large number of actions that have little to no value for a given state.

The Q-Network in this novel architecture is decomposed into two separate streams; a value stream and an advantage stream. Feature learning is carried out by a number of convolutional and pooling layers. The activations of the last of these layers are sent to both separate streams. Each stream contains a number of fully-connected layers. The final layer combines the output of the two streams, and the output of the network is a set of Q values, one for each action.

The aggregator for the two outputs of the advantage and value streams is: 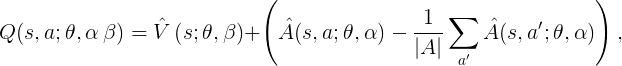dqn_aggregator

$\beta$ refers to the parameters specific to the value network, and the alpha refers to the parameters specific to the advantage network.

The advantage of the dueling network over standard Q-Networks is especially prominent when the number of actions is large. For standard Q-Networks, when the variation between actions is small, the Q-Network effectively has to learn the same value for all actions while each update only modifies the Q value of one action.

Evidence

The dueling network architecture outperformed the Double-DQN results in 50 out of 57 learned Atari games.

Strengths

The paper does a good job of making its main contribution (a novel neural network architecture) clear at the beginning.

The experimental algorithm for Dueling Networks employs other state-of-the-art advances in DRL (such as Double-DQN) which helps show the correlation between research being carried on in this field.

Increasing the action gap (Bellemare et al., 2016)

Notes

  • The value function V measures the importance of being in a particular state s. The Q-function measures the importance about the value of choosing each possible action when in this state. The advantage function, $A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s)$, subtracts the value of the state from the Q-function to obtain a relative measure of the importance of each action

  • A deep Q-network is a non-linear function approximator for the Q function having the form $Q(s,a;\theta)$ with parameters theta

  • We optimize the following sequence of loss functions: 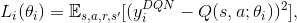dqn_loss with the target of the loss function, $y_i^{DQN}$, given by the reward signal plus the discounted maximal Q value provided by the target Q-Network

  • A target Q-Network that uses parameter freezing for a certain number of iterations is used to stabilize the algorithm

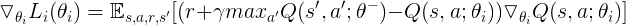
  • The specific gradient is dqn_gradient

  • Experience replay is used; use prioritized experience replay instead! (Don’t just sample uniformly from memory)

  • To avoid over-optimistic value estimates (van Hasselt, 2010), use Double Q-Learning. Originally, the max operator uses the same values to both select and evaluate an action. Instead, use the following target: ddqn