The Optimal Control of Partially Observable Markov Processes Over a Finite Horizon
Summary
This is the paper that revolutionized Partially Observable Markov Decision Processes (POMDP) research, coming out of Stanford and Xerox Palo Alto Research Center. They proved that, if there is a finite horizon for the control problem, the optimal value function is piecewise-linear and convex. I will present the proof and discuss possible connections with future work in Deep Reinforcement Learning.
Assumptions
- The underlying Markov process is a discrete-time, finite-state process.
- The number of possible outputs at each observation is finite.
- The reward output at each time step is not directly observed by the agent, but the extension to full observability is straightforward.
- The time horizon $T$ is finite.
Notation
- $a \in A(n) := $ the set of actions available at time $n$
- $p^{a}_{ij} := $ the state transition probability of moving from $i$ to $j$ when taking action $a$
- $r_{j \theta}^{a} := $ the probability of observing output $\theta$ if the new internal state of the process is $j$ under action $a$
- $w_{ij\theta}^{a} := $ the immediate reward accrued if the process transitions from states $i$ to $j$ under $a$ and observes $\theta$
- $\pi = [ \pi_{1} \pi_{2} … \pi_{n} ] := $ where $\pi_{i}$ is the probability that the current internal state of the system is $i$. $\pi$ is itself a discrete-time continuous-state Markov process. From a Bayesian perspective, $\pi$ is analagous to the current belief of the true hidden state.
Some POMDP Ramp-Up
If $\pi_{j}^{\prime}$ is the updated belief that the internal state is $j$, then it can be computed as
\[\begin{equation} \pi_{j}^{\prime} = \frac{\sum_{i} \pi_{i} p_{ij}^{a} r_{j \theta}^{a}} {\sum_{i,j} \pi_{i} p_{ij}^{a} r_{j \theta}^{a}} . \end{equation}\]This is the belief update, which follows simply by applying Bayes rule. The key thing to note is that $\pi$ is a sufficient statistic for computing $\pi^{\prime}$ (i.e., all of the information necessary to compute $\pi^{\prime}$ is contained in $\pi$). We can refer to (1) as
\[\begin{equation} \pi^{\prime} = T(\pi | a, \theta). \end{equation}\]If the expected immediate reward during the next time step starting in state $i$ under action $a$ is defined as
\[\begin{equation} q_{i}^{a} = \sum_{j, \theta} p^{a}_{ij} r_{j \theta}^{a} w_{ij\theta}^{a}, \end{equation}\]then the value function can be defined recursively as
\[\begin{equation} V_{n}(\pi) = \max_{a \in A(n)} \big [ \sum_{i} \pi_{i} q_{i}^{a} + \sum_{i,j,\theta} \pi_{i} p^{a}_{ij} r_{j \theta}^{a} V_{n-1} [ T(\pi|a,\theta)] \big] \end{equation}\]and is computed in a forward-backwards approach, as is common with Dynamic Programming algorithms. This equation can be interpreted as the maximum expected reward that the system can accrue until the end of the current process if the current belief state is $\pi$ and there are $n$ time steps remaining before the process terminates. Notice that by linearity of expectation, the value function is broken down into the sum of the expected immediate reward over the belief state (LHS of the sum), and the expected future utility over the belief state (RHS of the sum).
Since this is only valid for $ n \ge 1$, we can say that
\[\begin{equation} V_{0}(\pi) = \sum_{i} \pi_{i} q_{i}^{0} = \pi \cdot q^{0}. \end{equation}\]Where $q_{i}^{0}$ is the expected value of terminating the process in state $i$.
Proof that $V_{n}(\pi)$ is Piecewise Linear and Convex
We want to show the following:
\[\begin{equation} V_{n}(\pi) = \max_{k} \big [ \sum_{i = 1}^{N} \alpha_{i}^{k} (n) \pi_{i} \big ] \end{equation}\]for some set of vectors $\alpha^{k}(n) = [\alpha_{1}^{k}(n), \alpha_{2}^{k}(n), \ldots, \alpha_{N}^{k}(n)], k = 1, 2, \ldots$. To make the notation clear, note that a single $\alpha$-vector has $N$ components (one for each of the possible states the process could be in), and the $\alpha$-vector has a unique index $k$ referring to the region of the belief space that it partitions (more on this later). The index $k$ effectively enumerates the vectors as well.
We proceed by induction. (5) demonstrates that $V_{n}(\pi)$ has the desired form for $n=0$. Proceeding with the inductive hypothesis that $V_{n-1}(\pi)$ is of the form in (6), we shall show that this implies $V_{n}(\pi)$ is of the same form.
Let’s substitute (1), the belief update, into the term $V_{n-1} [ T(\pi|a,\theta)]$ from (4) such that
\[\begin{equation} V_{n-1}[ T(\pi|a,\theta)] = \max_{k} \big [ \sum_{j} \alpha_{j}^{k} (n - 1) \frac{ \sum_{i} \pi_{i} p_{ij}^{a} r_{j \theta}^{a}} {\sum_{i,j} \pi_{i} p_{ij}^{a} r_{j \theta}^{a}} \big ] \end{equation}\]It is important to see that $V_{n-1}( \cdot )$ is piecewise linear and convex, and that the belief simplex can be divided into a finite set of convex regions separated by linear hyperplanes such that $V_{n-1}( \pi ) = \pi \cdot \alpha^{k} (n - 1)$ within a region for a single index $k$. Let’s define $l(\pi, a, \theta)$ as the corresponding $\alpha$-vector index $k$ for the region in the belief simplex containing $T(\pi|a,\theta)$, the transformed belief state.
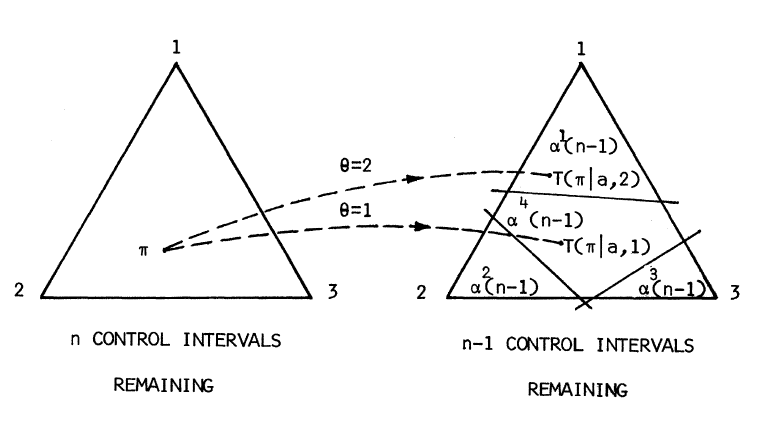
The belief-state update $T(\pi|a,\theta)$ for a simple POMDP, from Sondik, et al.
Notice in this image how the belief simplex, represented as a triangle where each vertex is one of the possible states, is partitioned into 4 regions by the set of $\alpha$-vectors at time-step $n - 1$. There are two possible measurements which transforms the previous belief $\pi$ to two possible new locations on the belief simplex.
Using $l(\pi, a, \theta)$ and (7), we can substitute into (4) to yield
\[\begin{equation} V_{n}(\pi) = \max_{a \in A(n)} \big [ \sum_{i} \pi_{i} [q_{i}^{a} + \sum_{\theta, j} p_{ij}^{a} r_{j \theta}^{a} \alpha_{j}^{l(\pi, a, \theta)} (n - 1) ] \big ]. \end{equation}\]To demonstrate (8) is piecewise linear and convex, we simply need to show that the bracketed quantity is piecewise linear and convex, since a maximum of a set of piecewise linear convex functions is itself piecewise linear and convex. First, note that for each $a$ and $\theta$, $l(\pi, a, \theta)$ is a finitely valued function of $\pi$. This, plus the fact that $V_{n-1}( \cdot )$ is assumed to be convex and the continuity of $T(\pi|a,\theta)$, implies that $l(\pi, a, \theta)$ partitions the belief simplex into a finite number of regions such that $l$ is constant in that region, as in the figure above. Holding $a$ constant in $l(\pi, a, \theta)$, we can take the union of all different partitions defined by varying $\theta$ to create a new region; the inner bracketed quantity is then constant over each of the partitions within this region; we are taking the expectation over all possible measurements, essentially. The result is that the outer bracketed quantity in (8) is piecewise linear over the belief simplex, with each different action $a$ contributing $K^{M}$ linear functions. $K$ is the number of $\alpha$-vectors at time step $n-1$ and and $M$ is the number of different possible measurements. While every $\alpha^{l(\pi, a, \theta) = k}(n - 1)$, $k = 1, 2, \ldots$ contributes new linear functions to (8), the majority of these regions (indexed by $k$) are dominated by the subset of vectors that are maximal. This will be important later on. By taking a maximum over $k$ in (7), we also ensure the convexity of the outer bracketed quantity in (8). Therefore, (8) is in the desired form of (6), and the proof is complete.
Discussion
Unsurprisingly, no one actually directly uses the above algorithm to do Value-Iteration to solve Reinforcement Learning problems; the time and space complexity of computing the value fuction by finding each $\alpha$-vector is mind-boggling. Starting from way back, most POMDP solvers would regularly prune the set of $\alpha$-vectors so that only ones which made up the maximal set (and were not dominated) were kept. By dominated, I simply mean that the hyperplanes corresponding to the dominated $\alpha$-vectors produce utility values for any given belief that are strictly less than the maximal set of $\alpha$-vectors.
However, over the years, many improvements to this approach have been made. Chiefly, the idea of Point-Based Value Iteration (PBVI) formalized the intuitions that the set of reachable belief-states for an agent is much smaller than the actual size of the belief simplex. In fact, for most problems, huge subspaces of the belief space are never reached. Many popular POMDP solvers that compute approximations to the optimal value function came from this idea, (e.g., SARSOP). From there, scaling up POMDPs to larger finite-world problems by using a tree-search approach to explore the belief simplex led to the complete abandonment of explicitly computing $\alpha$-vectors. Rather, many of these solvers opted to use Q-learning to avoid the value-function entirely, favoring the fast convergence times for bigger problems (and disregarding the deterioration in quality of solutions). There have been other approaches as well that fall into the camp of policy-iteration methods that perform well on certain problems.
Application to Deep Reinforcement Learning
Algorithms like DQN that assume the state is fully observable tend to work well when the state really is fully observable. Unsurprisingly, when the true state of the system is partially observable, the performance degrades significantly. When you apply DQN to environments where states are partially observable, it’s like you’re using a representative set of particles for modeling your current belief state distribution, as in PBVI, except the particle set size is fixed at 1.
Many people studying RL will agree that there is a long way to go until our agents can exhibit high-level cognitive functionality. The common consensus is that the most difficult tasks are going to be partially observable, and will require some form of memory and clever exploration motivated by intrinsic desires to handle sparse rewards.
So, is there any way to utilize our deep learning arsenal with traditional POMDP methods, which provide guarantees on convergence to the optimal value-function in partially observable environments?
For example, one could imagine reducing the dimensionality of the belief simplex sufficiently while simultaneously encoding the important information into some clever representation. Perhaps this could be done with a spatio-temporal approach in the general strain of Oh, et al., 2015, PCA, or an autoencoder. Another key component would be a learned model that could predict the corresponding set of $\alpha$-vectors for each action at the current time step; then, you could construct your value-function out of your predicted hyperplanes and encoded belief state. There would be all kinds of interesting geometry to exploit, given that the probability of being in many of the hidden states should be close to 0, which would collapse various dimensions of most of the hyperplanes. Additionally, you will want to learn a sparse set of linear hyperplanes, sort of how SVMs produce a sparse set of support vectors, since the only ones you care about are the maximal, dominating ones. The advantages of taking this route are abundant, one being that we would be able to get rid of many of the false assumptions that must be made when approximating POMDPs as MDPs, while at the same time preserving the scalability that deep learning has brought to RL.
Challenges
- One of the difficulties of this approach is that you would need to come up with a way to approximate the belief-update distribution. By using this distribution, that implies that this approach is inherently model-based as opposed to model-free, which appears to be another direction that some RL-practitioners seem to be gravitating back to.
- Another difficulty will be the representation of the belief state. Generally, a representative set of sampled particles that can be filtered through the system dynamics via Monte-Carlo methods is used. This would be good to avoid, since this adds unwieldy computational costs.
Note: There is some prior work on learning $\alpha$-vectors to obtain an approximation of the value function. Chiefly, a set of basis functions is supplied such that the $\alpha$-vectors can be factored into a linear combination of the basis functions and some weights.