RUDDER: Return Decomposition for Delayed Rewards
Arjona-Medina, Gillhofer, et al., 2018
Intro
Delayed rewards is one of the fundamental challenges of reinforcement learning. This paper proposes an algorithm for converting an MDP with delayed rewards into a different MDP with equivalent optimal policies where the delayed reward is now converted into immediate rewards. They accomplish this with “reward redistribution”—a potential solution to the RL credit assignment problem.
Basically, they argue that reward redistribution enables monte-carlo (MC) and temporal-difference (TD) methods to be applied under delayed rewards without high variance or biasing the Q-values. This is important, because TD methods are the most commonly used RL approach, and it is proven in this paper that with delayed rewards TD methods take time exponential in the length of the delay to remove the bias.
Some details about RUDDER
One of the main obstacles that is addressed in Section 3 is proving that the new MDP with redistributed rewards has the same optimal policies as the original MDP. I found that this section (and the previous) were unecessarily hard to read, but here is my take on what the key points are:
- Because the delayed reward MDP obeys the Markov property, the transformed MDP with equivalent optimal policies but immediate rewards needs to have an altered set of states. This altered set of states obey the Markov property for predicting the immediate rewards, but crucially, not for the delayed reward. This is accomplished by using differences between states $\triangle (s, s’)$ in the delayed reward MDP as the new set of states
- The return of the delayed reward MDP at the end of an episode should be predicted by a function $g$ (the LSTM) that can be decomposed into a sum over the state, action pairs of the episode
- It should hold that the partial sums that all together sum to $g$, $\sum_{\tau = 0}^{t} h(a_{\tau}, \triangle(s_{\tau}, s_{\tau+1}))$, equal the Q-values at time $t$ for the reward redistribution to be optimal
- This approach requires strong exploration that can actually uncover the delayed reward. If a robot gets a +1 for doing the dishes correctly and +0 reward otherwise, it may never even see the +1 in the first place!
- To help with the above, they use a “lessons replay buffer” to store episodes where the delayed reward was observed, to sample from when computing gradients for improved data efficiency
- An LSTM is used for the return prediction, and techniques for credit assignment in deep learning like layer-wise relevance propagation and integrated gradients are used for “backwards analysis” to accomplish the reward redistribution. This gets pretty complex, and the appendix goes into detail of how they modified the LSTM cell for this (something called a “monotonic LSTM”)
- They have to introduce other auxiliary tasks to encourage the reward prediction LSTM network to learn the optimal reward redistribution and get around the Markov property problem mentioned earlier. These aux tasks are to predict the q-values, predict the reward in the next 10 steps, and predict the reward accumulated from time 0 so far
Experimental results
The authors note that RUDDER is aimed at RL problems with (i) delayed rewards (ii) no distractions due to other rewards or changing characteristics of the environment (iii) no skills to be learned to receive the delayed reward. (iii) seems to imply that RUDDER could be combined with hierarchical RL. (ii) suggests that when there are sporadic rewards throughout an episode, the improvements from RUDDER might be minimized. Hence, the environments they experiment with all have heavily delayed rewards observed only at the end of the episode, and their results are naturally impressive. I understand the difficulty (high computational/$$$ cost) in evaluating on all 50-something Atari games, but it would be really nice to see how it fares on other games that aren’t perfectly set up for RUDDER.
They also note that human demonstrations could be used to fill the lessons buffer, which might further improve recent impressive imitation learning results.
Grid world
They compute an optimal policy for a simple grid world with a delayed reward MDP. Then, they compute the bias and variance from the mean square error (MSE) of the Q-values for MC and TD estimators with policy evaluation. They demonstrate the exponential dependency on the reward delay length for the MC and TD methods by varying the delay. RUDDER shows favorable reductions in the bias and variance of estimated vs. optimal Q-values at all delay lengths.
Charge-discharge
Simple 2-state and 2-action MDP with episodes of variable length and delayed reward obtained only at the end of the episode. RUDDER augmenting a Q-learning agent is much more data efficient than pure Q-learning, MC agent, and MCTS.
Atari evaluation
The most impressive results of the paper are the scores for the Venture and Bowling Atari games. They set new SOTA on Venture. They augment PPO with the return prediction network paired with integrated gradients for backwards analysis. The lessons buffer is used to train both the return prediction network and A2C (for PPO). I’m not sure about that because I thought PPO was an on-policy algorithm- using episodes from the lessons buffer would bias the policy gradient? They use the difference between two consecutive frames for $\triangle(s, s’)$ plus the current frame (for seeing static objects) as input.
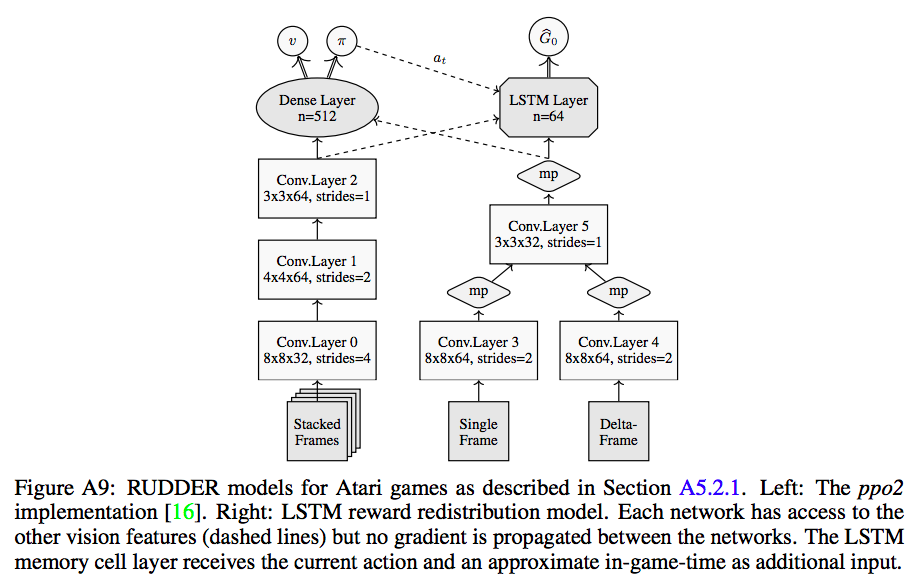
NN architectures for RUDDER augmenting PPO
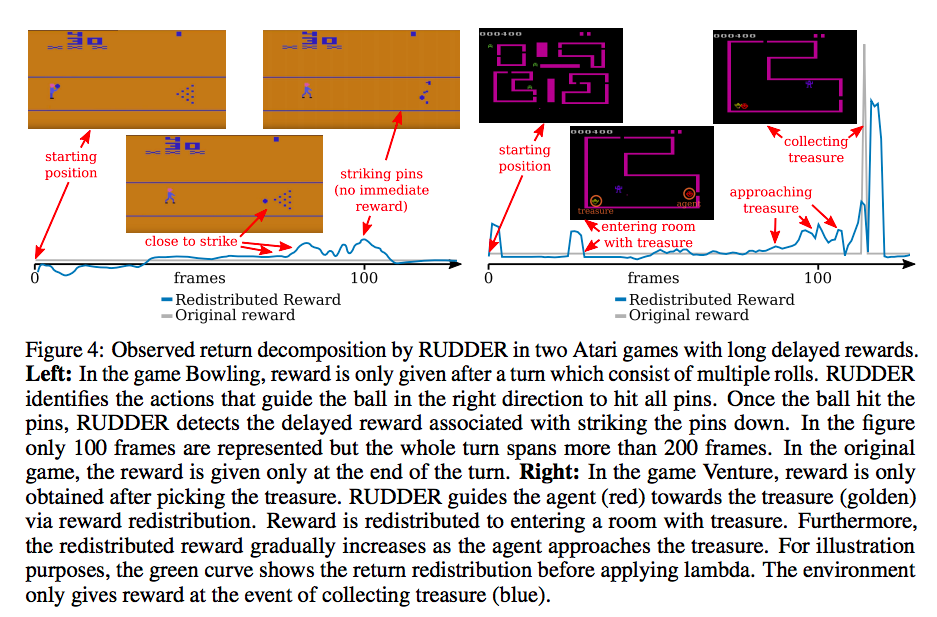
Visual depiction of the reward redistribution
They show that RUDDER is much more data efficient than APE-X, DDQN, Noisy-DQN, Rainbow, and other SOTA Deep RL approaches on these two games. Video.
Closing thoughts
I think this is an exciting RL paper that will have a major impact. Mainly because I can see lots of future research refining the ideas from this paper and then applying it to a variety of domains, especially in robotics. This paper could use polishing (some parts are not easy to read) and some more experiments showing how it performs on MDPs with both delayed rewards and also some other “distractor” rewards. I think this setting is most common, as it’s usually possible to do a little reward hacking to augment sparse/delayed reward MDPs. In the appendix, they go into the engineering details on how they got this to work, and it seems like that process + how the hyperparameters/auxiliary tasks/choice of method for backwards analysis will need to change for different environments will need to get cleaned up before making this approach widely useful.